Was the Rule of 18 Good Enough?
The spacing of the frets of fretted instruments was accomplished during the 19th century using mechanical proportioning. The math behind the technique is generally referred to as the rule of 18, in which the distance from the nut to first fret is determined by dividing the scale length by 18. The distance from the first fret to the second fret is determined by dividing the distance from the nominal bridge saddle location to the first fret by 18, and so on up the fretboard for all the rest of the frets. In more modern times this method has been replaced by math based on the 12th root of 2, which spaces the frets in the same proportion as the frequencies of the notes in equal temperament. This is assumed to yield more mathematically accurate fret spacing. This article tests that assumption using mathematical modeling, and finds that use of the rule of 18 yields slightly inferior intonation results, but that the difference is likely to be below the level of human perception. This article originally appeared in American Lutherie.
Initial appearance: December 21, 2021
Last updated:
July 19, 2025
Was the Rule of 18 Good Enough?
Copyright © 2017 R.M. Mottola
[This article originally appeared in American Lutherie #130.]
The 2008 GAL convention featured a great concert by Jim and Karen Buckland, Jim playing reproductions of 19th century guitars. From my own experience of that concert and from talking to other attendees I can assert that most folks were truly amazed that these small, gut-strung, ladder-braced guitars sounded so full and rich and loud – loud enough to stand up quite well to piano accompaniment. Although many things may have been going through the minds of members of the audience of this concert, one thing that probably did not enter our thoughts was that the intonation of the guitars could have been improved.
Jim also gave an excellent presentation at that convention on the subject of building 19th century instruments using 19th century building techniques. Fast forward to the 2014 convention, where Jim gave a short presentation on laying out fret spacing using the mechanical technique in use during the 19th century. The math behind the technique is generally referred to as the rule of 18, in which the distance from the nut to first fret is determined by dividing the scale length by 18. The distance from the first fret to the second fret is determined by dividing the distance from nominal bridge saddle location to first fret by 18, and so on up the fretboard for all the rest of the frets. Jim demonstrated how this was done back in the day, using a proportional divider with proportion set to 18:1. Use of the divider obviates the need to do a lot of mathematical division, which of course would have had to be done by hand in the days before calculators and computers.

Photo 1 – Jim Buckland demonstrates use of proportional dividers to layout fret spacing using the rule of 18 at the 2014 GAL convention. (photo courtesy GAL)
I don’t know of any documentation which indicates the first use of the rule of 18 for fret placement but the rule very likely was derived empirically early in the history of fretted instruments. It is probable that makers and players of lutes and similar instruments with tied frets observed the spacing ratio apparent on well-intonated instruments, and then used that ratio to quickly set up fret spacing for subsequent instruments
These days we conventionally base fret spacing on the twelfth root of two ( or ), the same value used to divide the octave into the twelve notes in equal temperament. From this we can derive a constant which can be used in the same successive division manner as described above for use of the rule of 18. That constant (to three decimal places) is 17.817. The derivation of the constant is described in detail in a nice article written by William Leirer in American Lutherie #96, and also in my book Building the Steel String Acoustic Guitar. Because 18 is greater than 17.817, its use as a fret placement divisor will result in frets that are located closer to the nut than if 17.817 is used. All else being equal, frets located using the rule of 18 will result in intonation which is flatter than if the twelfth root of two-derived constant is used. But all else isn’t equal in the manner in which instruments were laid out historically using the rule of 18, vs the way they are conventionally laid out these days using the twelfth root of two. Historically, the successive division method of calculating fret locations using the rule of 18 begins by dividing the actual distance from nut to bridge saddle by 18. The scale length is the actual length from nut to bridge saddle, with no added compensation at the bridge.
In contrast, when the successive division method of calculating fret locations using the modern twelfth root of two derived constant 17.817 is used, we begin by dividing the nominal scale length by 17.817. After the fret locations have been established we then move the actual location of the bridge saddle a bit further away from the nut. This is done to help compensate for the fact the pressing the strings down to the fretboard stretches them, and also because they have bending stiffness. Both sharpen pitch. If compensation is not added, all notes will intone sharp. Moving the saddle away from the nut a bit flattens all notes a bit and thus provides some measure of compensation. Again, compensation was not generally added during manufacture of historical gut strung instruments laid out using the rule of 18.
I’ve often mused about the possibility that intonation of historical instruments could in fact be as mathematically accurate as modern instruments laid out using twelfth root of two fret spacing and bridge compensation. Since rule of 18 spacing will result in flatter intonation, the possibility exists that this flattening will compensate for the sharpening effects described above. After hearing Jim Buckland’s instruments with fretboards laid out using the rule of 18 and noticing no intonation problems, I thought it would be interesting to test this hypothesis. Ideally such an experiment would measure and compare intonation for mostly identical instruments that differed only in the constant used to lay out the fretboard, and whether or not there was added compensation. But a less time-consuming option is to simply model intonation using available mathematical models designed for that purpose. A number of such models are available, and they are all more similar to each other than significantly different. A careful investigation on this subject is detailed in the article “Classic Guitar Intonation” by Greg Byers, published in American Lutherie #47 (available in Big Red Book of American Lutherie Volume 4, p.368) and a nice mathematical model is presented. Similar models can also be found in other sources, including Mark French’s book Technology of the Guitar, which I reviewed in American Lutherie #116 and is my current go-to source for guitar technical information. The model I used for the investigation described here is from the article “It's All About the Core, or How to Estimate Compensation” by Sjaak Elmendorp.1 Sjaak’s model is mathematically simpler than some others, but I think this simplicity reflects an appropriate and optimal level of accuracy for a model of a physical system that is full of variability. Another thing that predisposes me towards this one is that Sjaak’s article describes validation of the model, that is, the model was used to build instruments, the intonation of which were measured to determine just how accurate the model is. This is an important step when considering the use of any mathematical model for an actual building project. For the first order evaluation presented here, any of the published intonation models work just fine.
The accompanying figures show modeled intonation deviation for each fret of each string of a typical six string classical guitar with a 65cm scale length, typical action, and a typical nylon string set. Since this investigation was prompted by a 19th century instrument, it would be appropriate to model a gut string set instead, but it turns out that string (or for wound strings, core) stiffness, the string property used in the modeling equation that would be different for these string sets, does not differ all that much for nylon, gut or fluoropolymer strings. While on the subject of strings let me point out here that modeled intonation values would be considerably different for steel strings. Deviation values in the figure indicate deviation from mathematically perfect equal temperament intonation and are rounded to the nearest whole cent.
Four different modeled fret and bridge placement systems are shown for comparison. The red dots indicate intonation deviations for a fretboard with frets placed using the twelfth root of two on an instrument with no added bridge saddle compensation. As can be seen, intonation is sharp at the first fret and gets progressively sharper towards the bridge. As previously mentioned, this progressive sharpening is due to the stretching of the string required to press it to the fret, and also to its bending stiffness. Nylon and gut are relatively elastic materials, so this stretch and stiffness result in minimal initial pitch sharpening. The same is true for the wound strings of these string sets, which have either nylon or silk floss cores.
The green diamonds show intonation deviations for a fretboard with frets placed using the twelfth root of two on an instrument to which bridge saddle compensation has been added. Classical guitars typically use a straight saddle that is perpendicular to the instrument centerline, which effectively adds the same amount of compensation length to each string. I’m using a compensation value of 2.5mm here because that value resulted in the best average 12th fret intonation across all strings when modeled. You can see that added compensation noticeably reduces intonation error for all strings, and this of course is why most guitars feature some amount of compensation at the bridge. Notice also that although improved by the additional compensation, the G string still trends sharp. This is due to increased stiffness of this thick string. Folks will often add additional compensation to the classical guitar G string saddle location for this reason. Also noteworthy is that compensation does not completely eliminate intonation deviation across all frets. This is partially due to the use of a straight saddle. If separate compensation is used for each string, then intonation deviation can be substantially reduced. It may be prudent to keep in mind that the fact that this is not generally done for classical guitars may say something about what players consider to be tolerable or even perceivable levels of intonation deviation.
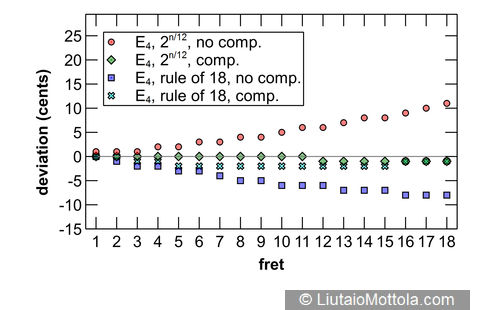
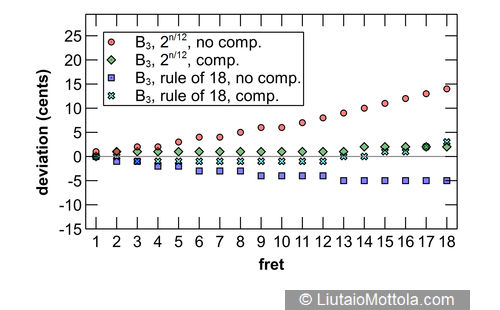
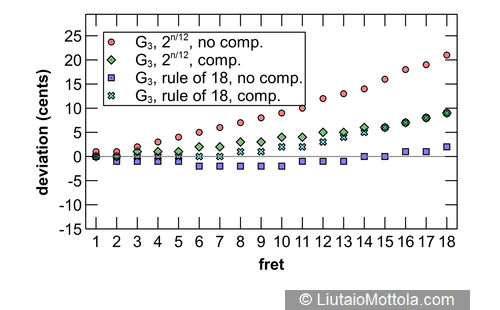
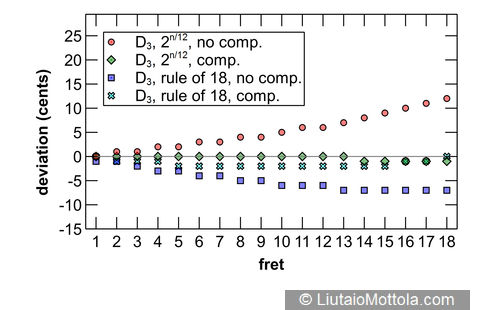
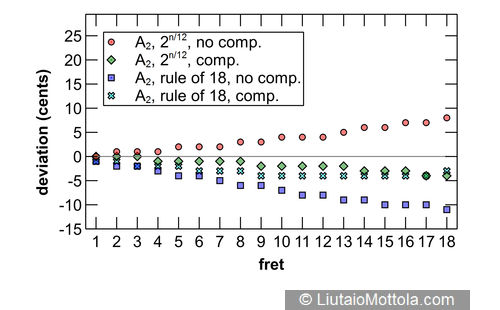
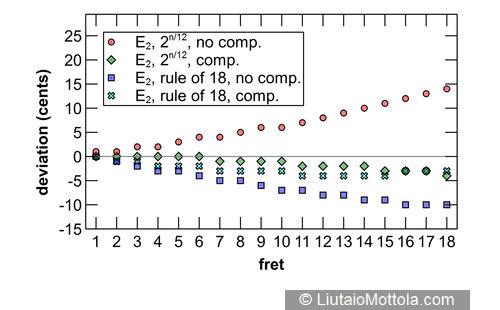
So the green diamonds show modeled intonation of a typical modern classical guitar and thus serve as the reference to which other fret placement systems are compared. The blue squares show intonation deviations for a fretboard with frets placed using the rule of 18 on an instrument with no additional bridge compensation. This is the typical configuration for a 19th century guitar and is the object of the hypothesis of this investigation. The hypothesis is that the progressive flattening of notes on fretboards laid out using this system could provide implicit compensation for the sharpening effects of pressing the string to the fret and of the string’s bending stiffness. But the modeling shows that the overall effect is for notes to trend flat. Comparing the twelfth root of two with compensation system to the rule of 18 system without compensation, it is apparent that the notes of the latter are always flatter than those of the former. And with the exception of notes on the G string, rule of 18 layout results in notes that generally deviate more from mathematically perfect intonation than if frets are laid out using the modern twelfth root of two with added compensation system.
Here’s an interesting thought experiment. Since rule of 18 without compensation yields notes that trend flat, it should be possible to sharpen them by moving the saddle closer to the nut. I have seen examples of such negative compensation added in an ad hoc manner – see for example the bridge of a Roudhloff brothers eight string guitar in James Westbrook’s article about those guitars in American Lutherie #129 and shown here in photo 2. I asked Jim Buckland if this style of negative compensation was ever used during manufacture of 19th century instruments. He told me that he was unaware of this being done with instruments having a bridge saddle, but for early 19th century instruments using lute-style bridges without saddles such as those by Gaetano Guadagnini, that it was common to adjust intonation by tying the string on with one or more loops around the vibrating part of the string (photo 3). Such an adjustment would effectively shorten the vibrating part of the string, implementing negative compensation.

Photo 2 – The bridge of an eight string guitar by the Roudhloff brothers. Note the negative compensation added on the first, second and fourth strings. This is obviously added after initial manufacture of the instrument. (Photo courtesy James Westbrook.)
A major advantage to the use of mathematical modeling in investigations such as this is the ease with which it is possible to try things out. The cyan crosses in the figure show the effect of subtracting 1.5mm of compensation on an instrument with frets positioned using the rule of 18. This value was chosen because it is the average diameter of the strings of a typical string set. As such it represents the average compensation that would be effected by adding a single loop around the vibrating length of the string when tying the strings to a saddle-less bridge. As you can see, although still generally flatter, notes of a modeled instrument using this system are much closer in pitch to those of a modern twelfth root of two with added compensation instrument, generally deviating by no more than two cents. It is interesting to note that by the late 19th century saddle-less guitar bridges all but disappeared, so the potential intonation advantages offered by this construction appear to have had little evolutionary impact.

Photo 3 – Detail of the saddle-less bridge of a reproduction of a Gaetano Guadagnini guitar by Jim Buckland. The front face of the bridge is located at exactly twice the distance from the nut as the 12th fret. Negative compensation is implemented by the tied loops over the vibrating length of the string, which effectively shortens that length. Adjustment of compensation is possible by adding more loops. The height of the top of the block above the string hole and the radius of the fillet of the leading edge of the block also affect the position of the loop.
Guitars evolved to make use of saddled bridges exclusively, so for the purpose of answering the question posed by this article’s title it is probably appropriate to focus on comparing results of the twelfth root of two with compensation system to the rule of 18 system without compensation. Various statistical analyses are possible but it is apparent just by looking at the figure that the modern system provides less intonation deviation for all strings other than the G string, given these modeled results, and thus is quantitatively more accurate. Although this may be of academic interest it is unfortunately not enough information to answer the question in a definitive manner for practical purposes. To do this we need two important pieces of additional information. The first is a measure of the intonation variability present in real guitars, and the second is a measure of intonation deviation that is perceivable by human listeners in musical contexts. These topics are too big to address here in detail, but I’ll touch briefly on them for folks wishing to pursue them.
The topic of variability in real instruments comes under the general heading of what in science and engineering is called significance. Results of a calculation, in this case intonation modeling, can be no more accurate than the least accurate input value. In the modeling performed above, all input values were optimal and so the calculations can only model intonation of a real instrument with perfect specs. But no real instrument has perfect specs. There are many sources of variability. The most obvious are related to the precision to which an instrument is manufactured, such as fret location and saddle location. Less obvious are those related to distortion of the instrument over time. Varying relief, action, and saddle location due to seasonal and permanent plastic deformation of the entire instrument can have substantial effects on actual intonation. Another source of variability is strings. Changes in string sets can substantially affect intonation as can manufacturing variability of the strings themselves. We generally use standard reference values or string manufacturers’ specs for string material stiffness and mass when such data are available, but these are often just rough approximations, provided by material manufacturers for structural engineering purposes. When such data are not available we most often derive values using rather crude home brewed measurement systems. Variability associated with playing the instrument is another factor. A guitar is hardly a rigid structure, and the act of playing it bends and distorts it in real time to some extent. It is also the case that a player does not apply the same fretting pressure each time a string is fretted, nor does a player consistently press the string straight down to the fret - fretting always involves some amount of inadvertent string bending.2, 3
So what we really need to do to answer the question posed in the title is to scrupulously collect all this real variability data and perform model calculations using the ranges of real data. The results would yield a range of intonation values for each fret instead of the single values of our simple modeling shown in the figures. Depending on the extent of those ranges, this could make the picture of superiority of one fret location system or the other a lot murkier.
Then there is the issue of human musical pitch discrimination. Humans do not have perfect musical pitch discrimination, and pitch deviations under the threshold of human discrimination are of no practical significance. This is a good place to point out that people generally and erroneously assume that at least some humans do have perfect musical pitch discrimination. This belief is generally due to the term traditionally used to describe the ability of some musicians to quickly identify the names of played notes without the aid of reference tones, “perfect pitch.” In fact musicians with this ability can typically only perform this to the nearest semitone. In reality there is nothing perfect about the pitch discrimination of those with this ability, and in fact they generally have no better pitch discrimination than do other trained musicians. For this reason this term is rarely used these days by human pitch perception researchers, and is replaced by the less confusing term absolute (as opposed to relative) musical pitch.
Human pitch perception has been widely studied and much is known about how it works. The subject is quite complex. Thick books have been written about it – the standard reference is a scandalously expensive psychophysics grad school text, appropriately titled Pitch. As generally measured for research purposes, general pitch discrimination is of little practical use to luthiers because there is no musical analog to the measurement technique. Research relevant to the task at hand is about a much more specific quality, human musical pitch interval discrimination. Research here is rather thin. It is also important to note that there is often a vast difference in the level of musical pitch discrimination humans can perform under research or tuning conditions and what we do perform in musical contexts, the latter being far more relaxed.
Unfortunately there is no single value for human musical pitch interval discrimination, and the range of that discrimination is extremely wide and is influenced by a bewilderingly large number of factors. The range extends from a possible minimum of 1 cent to a maximum of 50 cents. I calculated that lower bound as what could theoretically be achieved while tuning the high E string of a guitar. It is unlikely to be reliably realizable in any real musical context. It is also the advertised frequency resolution for typical digital tuners. In informal research (unpublished, small number of trained musician subjects) I performed in this area using recorded steel string guitar tones, presented as a major third interval near the center of the guitar’s pitch range and under ideal listening conditions, only one of the subjects could detect pitch interval deviations of 3 cents with even a little reliability. This value is probably much closer to what a likely lower bound would be in a musical context.
But given a 3 - 50 cent range and even considering that its lower bound is probably higher than 3 cents, we can make a few simple observations about the modeled data presented. The first is that straight saddle only compensation is probably good enough for modern classical guitars. With the exception of the G string, modeled intonation deviation is within that lower limit of human musical pitch interval discrimination over the entire range of the instrument. Adding separate G string compensation would put modeled intonation deviation for the entire instrument below that threshold of human musical pitch interval discrimination. I point this out here because, although not the focus of this article, a discrimination threshold applies to all attempts to improve intonation. The second observation is that instruments with frets laid out using the rule of 18 and no additional saddle compensation showed intonation deviation within that lower limit of human musical pitch interval discrimination over some of the range of the instrument for all strings, and over the entire range on the G string. Relax the above-stated 3 cent lower limit of human pitch interval discrimination to something much more likely to occur in a musical context and/or add saddle compensation, and such instruments may be indistinguishable from modern instruments as far as humanly perceived intonation goes.
Again, from an analytical perspective and given the modeled data presented here we can’t definitively answer the question posed in the title, “Was the rule of 18 good enough?” But let me conclude by repeating the empirical observation from the musical context made in the introductory paragraph of this article, for what it is worth. At the concert presented at the 2008 GAL convention the audience was enthralled by the playing of Jim and Karen Buckland, with nary a concern about intonation.
Acknowledgments
Jim Buckland, Tom Harper and January Williams kindly reviewed a draft of this article and provided great commentary. It is a wonderful thing to have such subject matter experts looking over my shoulder.
References and Suggestions for Further Reading
Elmendorp, Sjaak “It's All About the Core, or How to Estimate Compensation” American Lutherie, #104
Mottola, R.M. “Same-Fretted-Note Intonation Variability of the Steel String Acoustic Guitar” OSFPreprints, 2018
Mottola, R.M. “Quantifying Player-Induced Intonation Errors of the Steel String Acoustic Guitar” OSF Preprints, November 2019.


